Statistikk

Maskinlæring, data mining og ulike digitale verktøy er nødvendige for at vi skal kunne nyttiggjøre oss av data. I kjernen av det hele finner vi et begrep vi kjenner igjen fra både tippekuponger og barneskolepensum: statistikk.

Store Norske Leksikon definerer statistikk som vitenskapen om innsamling, oppsummering og analysering av data. Og det er jo egentlig i stor grad akkurat det vi snakker om, ikke bare i dette kapittelet, men i hele Datareisen!

Statistikk hjelper oss med å se sammenhenger i data. Metoder og teknikker fra statistikken, som klassifisering og regresjon, står helt sentralt innen områder som dataanalyse og maskinlæring. Statistikk er også det vi bruker for å kunne regne ut sannsynlighet, identifisere trender, og se sammenhenger i et datasett.

Når vi snakker om å jobbe datadrevet og setter det i en moderne sammenheng, blir datasettene ofte så enorme at de ikke gir mening uten å settes i sammenheng. Og da trenger man gode statistiske metoder.

I statistikken jobber vi ofte med store og uoversiktlige mengder med data. Deskriptiv statistikk er en del av statistikken som hjelper oss med å forstå og beskrive egenskapene til et datasett.

Ved hjelp av deskriptiv statistikk kan vi forstå dataene bedre, identifisere mønstre og trender og se etter likheter og forskjeller på tvers av ulike datasett.

Her er det en rekke teknikker og verktøy i spill, som du kan lese om i eksempelet nedenfor.

Der for eksempel gjennomsnitt og typetall er konkrete utregninger vi kan gjøre med kvantitative data, er sentralitet, spredning og moment litt bredere kategorier for hvordan vi jobber med deskriptiv statistikk.

Her vil en ofte kombinere de ulike teknikkene beskrevet ovenfor på ulike måter, avhengig av hva slags innsikter og sammenhenger en leter etter.

Sentralitet er deskriptive statistiske teknikker som handler om å representere det midterste eller vanligste punktet i en tallrekke eller et datasett. Eksempler på dette er å måle eller regne ut gjennomsnitt, median eller typetall.

Hvis dataene våre fordeler seg jevnt og symmetrisk, kan gjennomsnittet og medianen være nær eller fullstendig identiske. Men når vi derimot har såkalte skjevfordelte data vil median gi et annet – og ofte bedre – bilde av situasjonen enn snittet.

La oss se på et eksempel. Du husker kanskje fra tidligere at 93 prosent av Norges befolkning (i alderen 9-79) brukte internett en gjennomsnittsdag i 2021, ifølge SSB. I snitt brukte hver av oss 218 minutter på nett hver dag dette året. Altså 3 timer og 38 minutter.

Imidlertid kan vi forvente oss at internettbruken ikke fordeler seg helt jevnt i befolkningen. Unge mennesker som spiller, studerer og jobber online vil være mer på nett enn eldre generasjoner, og også mer enn de yngste, som har begrenset skjermtid. Ganske riktig: I SSB sine tall – der internettbruken er fordelt på fem aldersgrupper – er det de mellom 16-24 år som bruker nettet overlegent mest. De har et snitt på 340 minutter daglig, nesten seks timer.

Derfra går det gradvis nedover. Her har vi altså en skjevfordeling, og da kan median være mer treffende enn gjennomsnitt. I dette tilfellet er medianen 198 minutter – 20 minutter mindre enn snittet. Mer presist har vi det som kalles en «høyreskjev fordeling», om man skulle vist dette i en graf.

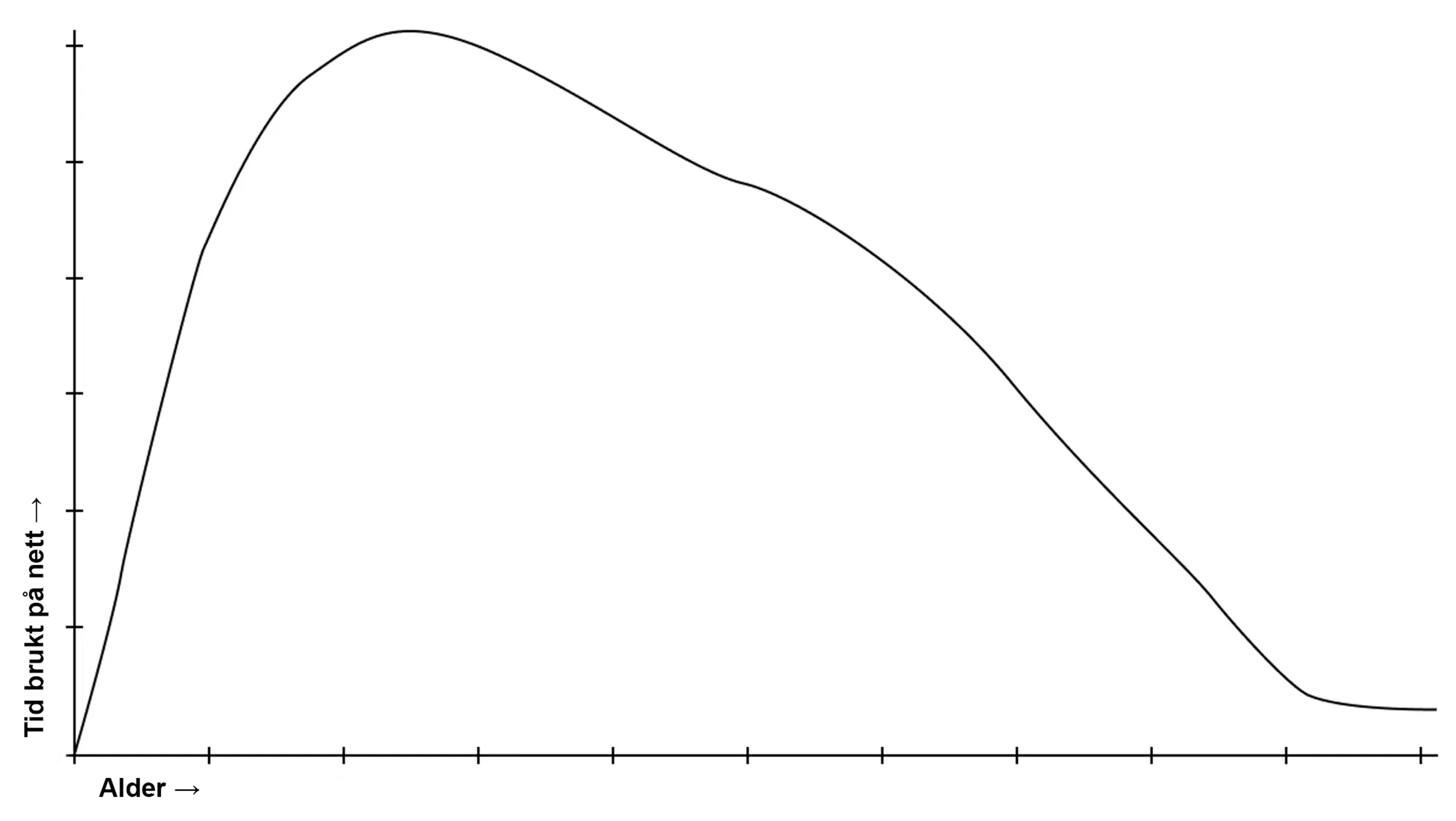
Hva med typetall? Som vi husker, er dette det tallet som forekommer oftest i datasettet.

I dette enkle eksempelet har vi egentlig bare fem tall å forholde oss til – antall minutter på nett for hver av de fem aldersgruppene. Ingen av tallene er identiske, derfor er ikke typetall like relevant her. Hadde vi derimot hatt tilgang på tall fra alle respondentene, kunne typetallet gitt enda et interessant perspektiv på situasjonen. Kanskje den typiske bruker – med det antallet daglige minutter som forekommer oftest – er tydelig større eller mindre enn både snittet og medianen? Det er en spennende innsikt.

Vi tar med oss enda et lynkjapt eksempel på sentralitet før vi går videre. Nemlig det at gjennomsnitt ikke nødvendigvis vil gi et riktig bilde av hva en typisk person har i inntekt. Dersom noen i den aktuelle gruppen håver inn millioner, mens de fleste andre har en mer moderat lønn, vil det gi en skjev fordeling i stedet for en jevn og symmetrisk kurve. I dette tilfellet vil det være en venstreskjev fordeling – motsatt av grafen over internettbruk. Her kan median og typetall være interessante å se på, og gi oss annen og mer nyansert informasjon enn det vi får ved bare å se på gjennomsnittet.

Som en slags motpol til sentraliteten finner vi spredningen. Dette er en sekkebetegnelse for teknikker som måler hvor mye verdiene i et datasett varierer. Eller sagt litt enklere: hvor ulike og hvor langt de står fra hverandre.

Om vi ser på listen vår ovenfor, faller både variasjonsbredde, persentiler, prosenter og standardavvik inn i denne kategorien.

For at disse skal være interessante, gjelder det å stille de riktige spørsmålene. Eksempelvis er det ikke nødvendigvis så veldig nyttig å vite variasjonsbredden i et datasett dersom det største tallet ligger milevis over de fleste andre verdiene.

Ta eksempelet med inntekt, igjen. Si at vi skal se hvordan det har gått økonomisk med en skoleklasse etter 20 år. Én av avgangselevene er blitt søkkrik og tar ut store summer hver måned, mens de andre har en mer normal inntekt. Her vil variasjonsbredden riktignok bekrefte at det er store forskjeller, men den vil i liten grad si noe interessant om inntekten til de fleste i skoleklassen. For at variasjonsbredden skal være et godt mål for spredningen, bør verdiene variere jevnt og gjerne over et relativt lite område.

På samme måte bør en persentil vektes med omhu slik at den ikke feilrepresenterer datasettet. En persentil er altså i praksis når man deler et datasett i hundredeler, og deretter måler verdier opp mot dette for å se om de faller innenfor denne bestemte prosentandelen. Medianen tilsvarer som nevnt 50-persentilen, så halvparten (50 prosent) av verdiene vil her være mindre enn eller lik medianen.

Dette er nyttig for eksempel innen vekt- og aldersstatistikk. Si at et barn skal følges opp og veies ettersom hun blir eldre, for å finne ut om hun er under-, normal- eller overvektig i forhold til alderen. 50-persentilen er da normalvektig, mens 25-persentilen er undervektig. Så om hun faller på 37-persentilen, er hun et sted i mellom disse to.

Her er det viktig at datakvaliteten er god, for om disse tallene flyttes på (for eksempel hva som regnes som normalvektig) kan man fort ende opp med et feilaktig bilde av sin egen vekt og hva denne betyr. Variabler som høyde og fettprosent må også tas hensyn til, ellers kan et veldig høyt eller veltrent individ fort ende opp som overvektig dersom man kun ser på vekt og alder.

Kort fortalt: Når vi bruker disse teknikkene, er det viktig å ikke bare kjenne til hvordan vi gjør selve regnestykkene – men også å forstå og kunne tenke kritisk rundt hva resultatene betyr. Vi må evne å stille de riktige spørsmålene, være trygge på at datakvaliteten er god nok, og være obs på hvilke ting som kan gjøre at det svaret vi får ikke nødvendigvis forteller det riktige eller hele bildet.

Én måte å nyansere bildet på kan være å se på standardavvik. Det handler altså om å sette et tall på hvor langt verdier typisk avviker fra gjennomsnittet.

Her kan vi gå tilbake til eksempelet ovenfor med daglig internettbruk i befolkningen. En enkel formel i Excel viser oss at standardavviket her er på 99 minutter. Det vil si at hver av de fem aldersgruppene i snitt bruker nettet enten 99 minutter mer eller mindre enn det samlede gjennomsnittet.

Dersom det var veldig små forskjeller på internettbruken mellom de ulike gruppene, ville dette tallet vært mye lavere. Når standardavviket imidlertid er på over 1,5 time, forteller det oss mye om hvor stor forskjell det er i tiden brukt online på tvers av generasjonene.

I de to kategoriene over snakket vi hovedsakelig om enkeltverdier, og om å gi dem mening sett opp mot datasettene de var en del av. I denne delen er det i større grad snakk om å se trender i hele datasett, og en av de mest populære måtene er gjennom det som omtales som «moment». Dette er hentet fra en matematisk idé fremmet av den britiske matematikeren Karl Pearson, og er bedre kjent som Pearsons produkt-moment korrelasjonskoeffisient (og andre buskevekster – prøv å si det der fort fem ganger!).

Du har sikkert sett eksempler på nokså tullete statistikk, der to helt urelaterte typer data settes opp mot hverandre og presenteres som om de har en sammenheng. Eksempelvis har noen funnet ut at global oppvarming har en nesten perfekt korrelasjon med nedgangen i antall sjørøvere de siste to hundre årene, noe som ikke gir særlig mye mening.

Dette er nettopp to datasett satt i sammenheng. Det kan enkelt fremstilles som et årsak-virkning-forhold, men det er selvsagt en feilslutning.

Det som er feil er her er ikke selve regnestykket. Feilen er å konkludere med at det finnes en årsakssammenheng i det som bare er en absurd tilfeldighet. Her har man ulike bakenforliggende årsaker som gjør at det feilaktig ser ut som det er en samvariasjon.

Selve målet på korrelasjonen, altså den lineære grafen som viser sammenheng, er det som kalles kovariasjon. Hvor mye varierer to datasett fra hverandre, og hvor mye henger de sammen? Samvariasjonen kan være positiv (grafene følger hverandre) eller negativ (hver gang én graf svinger opp, går den andre ned).

At Justin Biebers alder viste en nær sagt perfekt korrelasjon med fallende kolesterolverdier i befolkningen – men at denne trenden snudde i omtrent perfekt motsatt retning så fort Facebook ble lansert – er ikke bare nok et tullete eksempel på en tilsynelatende korrelasjon uten årsakssammenheng. Her går vi også fra å ha en negativ til en positiv kovariasjon, ettersom kolesterolet først sank, og deretter steg, i perfekt rytme med sangerens alder.

Slike datasett kan også representeres enklere, som en såkalt korrelasjonskoeffisient, som vi nevnte i forbindelse med Pearson. I denne benyttes både standardavviket til datasettene og deres kovarians, for å finne en «ekte» indikator på korrelasjon. Det er i en slik utregning at de spuriøse eksemplene over fort ville falt i fisk.

Slik brukes altså statistikk for å verifisere og sjekke verdien i datasett, og sørge for at man kan stole på dem – og i siste instans anvende kunnskapen til å ta valg som har konsekvenser i virkeligheten.

Dette henger nært sammen med sannsynlighetsregning, og det er det neste vi skal se på.