Bits and Bytes
It's easy to forget that there are very tangible and physical processes behind everything that happens in the digital world: Ultimately, it's all just electrical signals buzzing around in wires and circuit boards—in physical machines made of plastic and metal.
So how do these machines actually work? A PC essentially consists of a processor and memory, in addition to input and output devices such as a monitor, mouse, and keyboard. This is called hardware. In addition, we need to provide precise and specific instructions for what the machine should do at any given time. This is called software.
Tying it all together is an incredibly large amount of electrical signals.
These signals are the famous 0s and 1s—electrical circuits, where there either is a signal (1) or no signal (0) at any given time. When a developer writes code with instructions for the computer, this will be translated under the surface into machine code (0 and 1), which is the only thing the machine can actually understand.
Such a signal is what we call a bit. It's short for “binary digit”, that is, a number in the binary numeral system, or the base-2 system. A bit has only two states: off (0) or on (1).
We need to get a little more familiar with this system to understand what digital data actually is, and how the digital world is connected.
Insight
How does the binary numeral system work?
A single bit doesn't do much, but in combination with other bits, it forms the foundation of the entire digital world.
The key to understanding why this is so ingenious, is that we can use software to get bits to represent practically anything. And it doesn't take many bits to create quite complex instructions—due to the “magic” of exponential numbers.
You may have heard the story of the man who asked for one grain of rice for the first square on a chessboard, two grains for the second square, four for the third, eight for the fourth—and so on? That is, a doubling for each of the 64 squares on the board. It sounds like a fairly humble request ... until you start doing the maths: By the time you get to the last square, you're talking about 18,446,744,073,709,551,615 grains of rice!
It's exactly the same principle that makes the combinations of 0s and 1s so clever: For each bit you add, you double the total number of possible combinations you get to work with. With one bit, you have only 2 possible states, but with two bits, you have 4, three bits give 8, four bits give 16, five bits give 32 ... and before you know it, you're up in the millions and billions.
And these combinations can be programmed to represent anything. For instance, a series of signals, like 01101101, can tell the machine to give you the letter “m” when you're working in a word processing software. While exactly the same eight bits can represent a shade of red, green or blue (RGB) in a pixel in a digital image file. This is how hardware (the machines and the electrical signals) and software (the instructions and rules for what these signals should represent) work together to create the entire digital reality.
Learn to count in binary
Let's pause briefly to better understand how the binary system actually works.
Imagine you have a box of Lego’s, and you're wondering how many bricks there are. You don't have anything to write on, and you start counting on your fingers ... but you can obviously only count up to ten. That's just a tad bit too little! With binary numbers, however, you can count all the way to 1023 (or 1024 if you count 0).
As you've now understood: What matters is not the number of fingers you have to count with, but the number of possible combinations of those ten fingers.
We can easily calculate the number of possible combinations using simple exponentiation, with 2 as the base and the number of bits as the exponent. The number of possible combinations with ten fingers is then two raised to the power of ten, i.e. 2^10 = 1024.
What if we include our toes as well, and thus work with a total of 20 bits? Maybe we’ll get a few thousand more? Well, it's easy to check: Two raised to the power of twenty is … 1,048,576!
Try it yourself ... by counting to 1024 using your fingers!
Want to see how it works? It is actually quite simple—and fun—once you understand the logic. It's also a great party trick if your friends are as cool and nerdy as you.
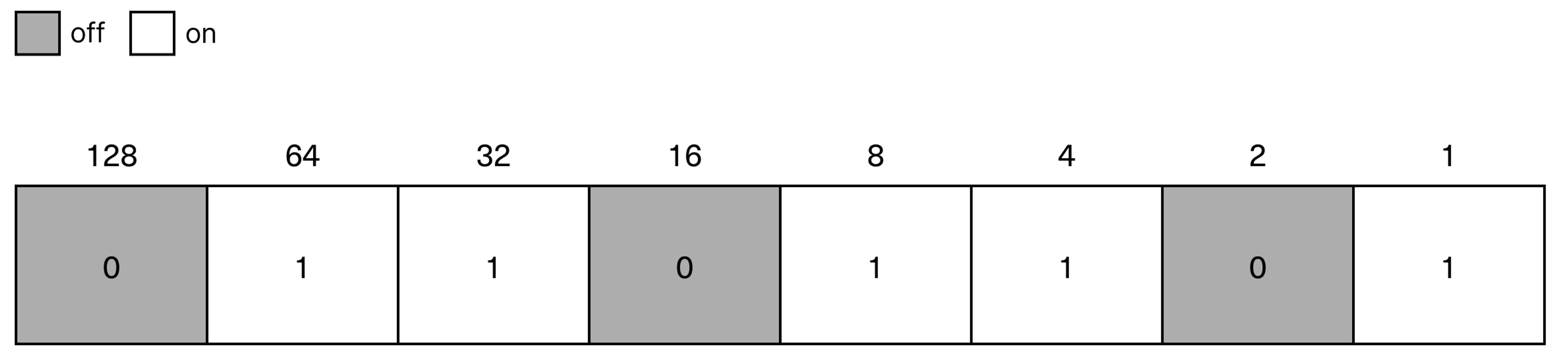
Bytes: Combinations of bits
Just as letters need to become words to convey anything, we create combinations of bits to accomplish something on a computer. The combination of eight bits is what's called a byte. A byte can represent 256 different values (2^8 = 256).
Each letter and each number you see here are represented by one byte in the computer's basic code. Bits and bytes can represent anything, not just numbers, but also letters, colours, sounds, customer data, football results, or anything else.
1000 (some would say 1024) bytes is a kilobyte, 1000 kilobytes is a megabyte, 1000 megabytes is a gigabyte, and so on. There are over a billion bytes (i.e., more than eight billion bits) in a gigabyte The number of possible combinations in a gigabyte would, more or less, give us a larger number than we have space to write here.
Everything you have on your computer—pictures, programs, text documents—is stored and processed this way, as compositions of bits and bytes. It's these compositions we use to represent different things in data.
How a machine works with bits and bytes
It's the computer's software that tells the hardware what to do with the electrical signals it receives (i.e. bits) in different contexts.
For example, if you're working in a word processing software and press the letter “m” on the keyboard, the machine, as mentioned earlier, receives the signals 01101101. As you now can see, this is one byte (eight bits). The software tells the machine that when it receives exactly these signals, it should create an “m” in your text document.
If you count, using the system you learned for counting on your fingers, you’ll find that 01101101 equals the number 109. Then you'll be pleased to learn that the so-called ASCII code for a lowercase “m” is indeed 109.
The ASCII character set (short for American Standard Code for Information Interchange) is a standard for how numbers, letters and other input from a keyboard should be represented as digital data. The standard was introduced as early as 1963, and is still in use today as part of the newer standard UTF-8 (Unicode Transformation Format 8, a variant of the Unicode character set).
Standards like Unicode ensure that the machine knows what to do with the signals it receives. We’ll take a closer look at how the machine is actually built and works, and how it receives commands, in the next topic.