Probability
Statistics are often used as a basis for decision-making in modern businesses, organisations, and government bodies. Precisely what is best or most advantageous to do in a given situation is usually difficult to know in advance. But through good use of data and statistics, we can, in many cases, still make decisions based on what is most likely to result in the desired outcome.
Probability was for a long time a fairly elusive concept. For most of human history, instead of calculating probability, we have relied on faith, destiny, and luck.
In many ways, we can thank gamblers and hazard players from the 17th century for taking probability calculation seriously. These activities can lead to large rewards, and the road to these rewards is paved with luck and—precisely—probability calculations.
It was in the pursuit of such rewards that three Frenchmen around the middle of the 17th century turned to the well-known French mathematician Blaise Pascal. At this time, it was an established “truth” that in a dice game with two dice and 24 throws, one could quite safely bet that at some point one would roll double sixes. But in Pascal’s calculations, it was seen that this was not a likely outcome; quite the contrary.
In addition to this somewhat simpler question, the Frenchmen also asked a question about how the pot should be fairly distributed if the game was stopped before it was finished. If it had been predetermined that the winner would collect the entire pot, then what if the game was interrupted? There was no rule for how the pot should be distributed based only on how likely it was that each player would have won.
Pascal solved this problem in correspondence with another mathematician, thus laying the foundation for modern probability theory. The solution? What we today know as expected value. The value is not identical with an actual outcome, but it approximates the average of the actual outcomes if the events had been played out.
Probability allows us to handle uncertainty
Today we use computers to calculate probability and simulate outcomes in different situations. In a computer program, one can perform millions of simulations of Pascal’s dice throws in an instant, thereby quickly and easily providing a good basis for decision-making. This means we can use probability calculation to help us with much more complex calculations than were possible in Pascal’s time.
Example
Throwing dice
There are many ways to illustrate probability, but the dice roll is a simple and understandable example. In the illustration below, you can see the result of us running 10,000 simulations of two dice rolls using an openly available tool (GeoGebra). The sum of the eyes on two dice can range from 2 to 12 on a throw. The diagram shows how the sum of the dice was distributed over 10,000 throws.
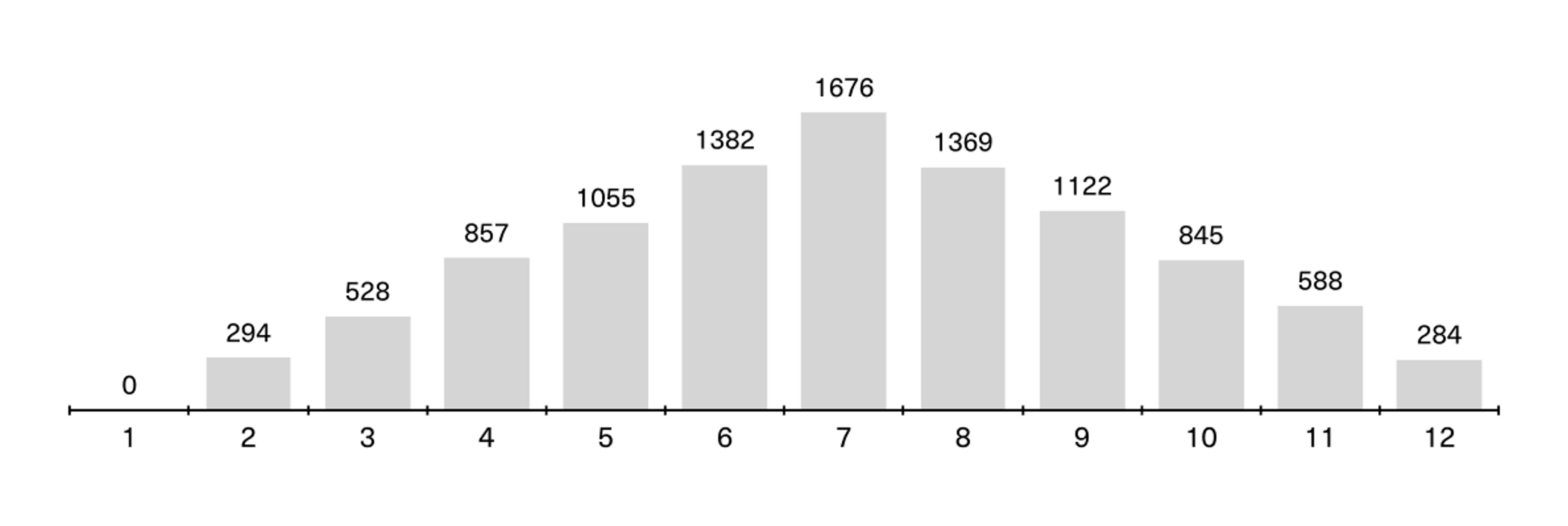
If we go back to the example of double sixes from Pascal’s example, we can see that out of 10,000 throws, there were only 284 instances where double sixes were the outcome. (Here, by the way, you see a good example of a normal distribution!).
Or in other words: there’s about a 2.8 percent chance of rolling double sixes on any given throw. As we touched on earlier, this probability applies to a single throw of a die, and not across the 24 throws the game consists of.
This naturally applies to all other variants of double numbers. If you add another die, the chance drops to about 0.5 per cent. But if you bet that the sum of two dice will end up with the value 7, you’ll have relatively good odds; a whopping 16.7 percent! That’s because you can get this result in several ways, whether you throw 1+6, 2+5, or 3+4.
If you were a Frenchman, a gambler, and wanted to get the most return for your money, it was therefore high stakes to bet everything on double sixes.
This illustrates the reason why many today emphasise the explosive power of digital tools, and the enormous forces we now handle when we work data-driven. Where we have access to sufficient data of good quality, we can use probability calculations to simulate how various situations and processes are likely to play out, and in the next instance use this to make better decisions. This is an important reason why data can be so valuable for businesses, organisations, and government agencies.
As you see, this is largely about handling uncertainty. How many cars will the car dealer sell tomorrow? Two, fifteen, none or three hundred? We don’t need to guess, but can use data and calculations to come up with a good answer. How many cars she sold yesterday, last month and this time last year takes us a part of the way. Then you can start to look for other factors that might come into play: perhaps the car dealer is aided by good weather, advertising campaigns, an upswing in the economy and a premiere of a blockbuster car film.
Here you must look for and evaluate correlations and causal relationships, and pretty soon you are in the process of putting together an intricate calculation—which can ultimately provide a more or less precise estimate of likely sales. Or in other words: a simulation.
Machine learning is often used for such calculations and simulations today. With the help of machine learning, we can map patterns in large data sets that it would typically have been highly unlikely for us humans to identify on our own—such as what factors really influence the sale of cars. Maybe it turns out to be completely different things than you intuitively thought. But the answers are there, in the data.
In this way, data-driven work can reveal and illuminate truths that would otherwise have remained obscured to us humans, and give us the ability to act and the basis for decisions to make better choices and influence the outcome of our work in a more desirable direction.
Our world, viewed through the lens of uncertainty and probability
Statistical inference
As mentioned, probability theory is about reducing uncertainty, not eliminating it completely. Even with powerful computers and millions of simulations, calculating probability will (probably) never become an exact science. This is actually quite obvious; we can rarely be completely certain about anything. But if a hundred percent guaranteed predictions or findings were a prerequisite for scientific progress, we would live in a quite different society than we do today. Most processes would probably stop before they even started if a certain degree of uncertainty was not accepted.
Moreover, we will usually never have access to absolutely all relevant data about a thing. When we are going to investigate something that is large and unmanageable, we therefore often draw out limited samples from larger populations—a so-called representative sample. Representative samples are typically used in surveys, and a similar technique is often used in dealing with other types of data sources.
What we are talking about here is so-called statistical inference, where conclusions are drawn about a larger group based on a limited sample. Such a group is often referred to as a “population”, meaning a specific number of individuals or objects with some common characteristics.
"Inference” for its part refers to a conclusion one makes by using logical reasoning based on the information at hand. Statistical inference is therefore a more discretionary assessment of the probability that something is true in a larger population, rather than a simulated calculation.
This is often used in the evaluation of medicines, for example. When a new vaccine is rolled out in a population, it’s difficult to say how effective it will be on the population as a whole. Therefore, a representative sample of the population is made, and the findings from this sample are scaled up to the rest of the population. Then you can say something about the vaccine’s effect and, for example, the likely expenditure the disease (that the vaccine is supposed to protect against) will amount to, or how likely it is that someone will become seriously ill from being infected after being vaccinated.
Statistical inference can be done using many different methods. In the next topic, on machine learning, we will delve into one of them: regression analysis.