Statistics

Machine learning, data mining, and various digital tools help us make the most of our data. At the core of it all, we find a concept we recognise from both betting coupons and the primary school curriculum: statistics.

The Great Norwegian Encyclopedia defines statistics as the science of collecting, summarising, and analysing data. And that’s really to a large extent what we’re talking about, not just in this chapter, but throughout the entire Data Journey!

Statistics show us patterns in data. Methods and techniques from statistics, such as classification and regression, are absolutely central within areas such as data analysis and machine learning. Statistics is also what we use in order to calculate probability, identify trends, and see connections in a dataset.

In the digital age, datasets often become so huge that the data makes no sense unless placed in context. That’s where good statistical methods come in, helping us make sense of it all.

In statistics, we often work with large and unwieldy amounts of data. Descriptive statistics is a part of statistics that helps us to understand and describe the characteristics of a dataset.

With the help of descriptive statistics, we can better understand the data, identify patterns and trends, and look for similarities and differences across various datasets.

There are a number of techniques and tools at play here, which you can read about in the example below.

Things like averages and modal values are concrete calculations we can perform with quantitative data. Centrality, spread, and moment, on the other hand, are slightly broader categories of how we work with descriptive statistics.

One will often combine the different techniques described above in various ways, depending on what kind of insights and correlations one is looking for.

Centrality refers to descriptive statistical techniques that involve representing the middle or most common point in a series of numbers or a dataset. Examples of this include measuring or calculating the average, median, and mode.

If our data is evenly and symmetrically distributed, the average and median may be identical, or close to it. However, when we have so-called skewed data, the median will provide a different—and often better—picture of the situation than the mean.

Let’s look at an example. You may remember from earlier that 93 percent of Norway’s population (aged 9-79) used the Internet on an average day in 2021, according to Statistics Norway. On average, each of us spent 218 minutes online each day that year. That’s 3 hours and 38 minutes.

However, we can expect that Internet usage is not distributed evenly across the population. Young people who play computer games, study, and work online will be online more than older generations, and also more than the youngest, who have limited screen time. Quite right: in Statistics Norway’s figures—where Internet usage is tracked across five age groups—we see that those between 16-24 years of age use the Internet far more than the rest. They are averaging 340 minutes per day, nearly six hours.

From there, it gradually decreases. So, here we have a skewed distribution, and in such cases, the median can be more accurate than the average. In this case, the median is 198 minutes—20 minutes less than the average. More precisely, we have what is known as a “right-skewed distribution”, if one were to show this in a graph.

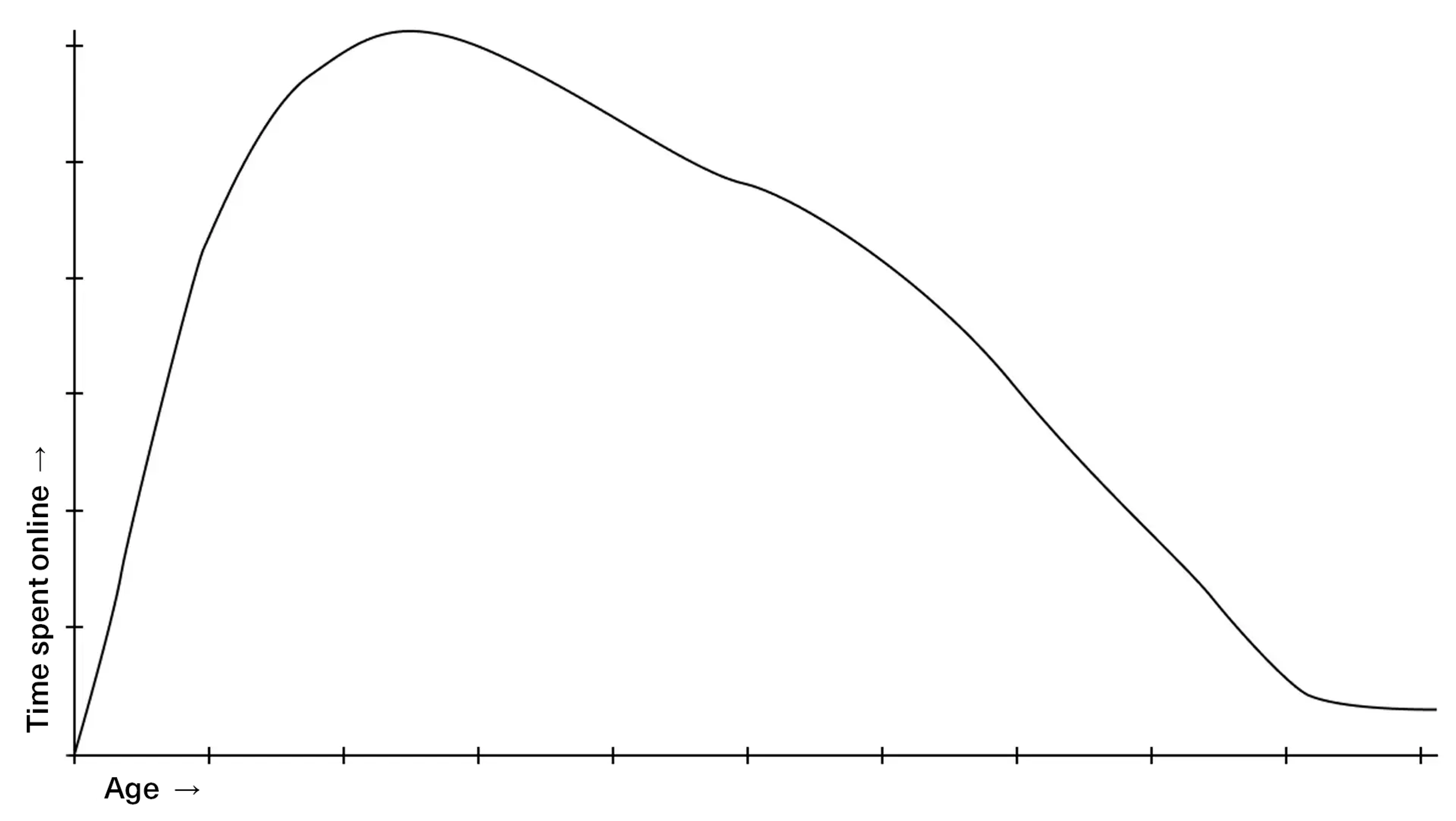
What about the mode? As we recall, this is the value that occurs most frequently in the dataset.

In this simple example, we really only have five figures to deal with—the number of minutes online for each of the five age groups. None of the figures are identical, so the mode is not as relevant here. However, if we had access to figures from all respondents, the mode could have offered an additional interesting perspective on the situation. Perhaps the typical user—with the number of daily minutes that occurs most frequently—is noticeably larger or smaller than both the average and the median? That’s an exciting insight.

We’ll look at one last quick example of centrality before moving on. Namely that averages do not necessarily provide a correct picture of what a typical person earns. If someone in a group rakes in millions, while most others have a more modest income, this will create a skewed distribution instead of a smooth, symmetrical curve. In this case, it would be a left-skewed distribution—the opposite of the Internet usage graph. Here, the median and mode could be interesting to look at and provide us with different and more nuanced information than what we get by just looking at the average.

As a kind of counterpart to centrality, we find dispersion. This is a generic term for techniques that measure how much the values in a dataset vary. Or put a bit simpler: how different they are and how far apart they stand.

If we look at our list above, both range, percentiles, percentages, and standard deviations fall into this category.

In order for these to yield interesting insights, it’s all about asking the right questions. For instance, it’s not necessarily that useful to know the range in a dataset if the highest number is miles above most other values.

Take the income example, again. Say we’re looking at how a class has fared financially 20 years later. One of the former students has become incredibly rich and has a huge salary, while most others have a more standard income. Here, the range will indeed confirm that there are large differences, but it will not say anything particularly interesting about the income of most of the students in the class. For the range to be a good measure of dispersion, the values should vary evenly and preferably over a relatively small range, without such extreme outliers.

Similarly, a percentile should be weighted with caution so that it does not misrepresent the dataset. Using percentiles, as you remember, basically means converting the values in a dataset into fractions (hundredths), and then checking what values fall within a particular percentage range. For example: The median corresponds to the 50th percentile, so half (50 percent) of the values here will be less than or equal to the median.

This could be useful, for example, in statistics about weight and age. Say a child is to be followed up and weighed as she grows older, to find out whether she is underweight, normal weight, or overweight relative to her age. The 50th percentile would be considered normal weight, while someone at the 25th percentile would be underweight. So if she falls on the 37th percentile, she’s somewhere in between these two.

Here, as always, it’s important that the data quality is good. If we change, for example, what is considered normal weight, one could easily end up with an erroneous picture of one’s own weight and what it means. Variables such as height and body fat percentage also need to be taken into account, otherwise a very tall and/or muscular individual could easily—and erroneously—end up being considered overweight.

In short: When using these techniques, it is important not only to know how to do the calculations—but also to understand and be able to think critically about what the results mean. We must be able to ask the right questions, be confident that the data quality is good enough, and be aware of things that can make the answer we get not necessarily tell the correct or complete picture.

One way to nuance the picture may be to look at the standard deviation. In other words, putting a number on how far the values in the dataset typically deviate from the average.

Here we can go back to the example above with daily Internet use in the population. A simple formula in Excel shows us that the standard deviation here is 99 minutes. That is, each of the five age groups on average uses the Internet either 99 minutes more or less than the total average.

If there were very small differences in Internet use between the different groups, this number would have been much lower. However, seeing as the standard deviation is more than 1.5 hours of Internet use per day, it tells us a lot about how big a difference there is in the time spent online across generations.

In the two categories above, we mainly talked about individual values, and about giving them meaning compared to the datasets they were part of. In this section, it is more about seeing trends in the entire dataset, and one of the most popular ways is through what is called “moments”. This is taken from a mathematical idea put forward by the British mathematician Karl Pearson, and is better known as Pearson’s product-moment correlation coefficient (yeah, it’s a mouthful!).

You have probably seen examples of rather silly statistics, where two completely unrelated trends in data are shown side by side and presented as if they have a correlation. For example, some have found that global warming has an almost perfect correlation with the decline in the number of pirates over the past two hundred years, which doesn’t make much sense.

These are, precisely, two datasets put in context. It can easily be presented as a cause-effect relationship, but that is of course a false conclusion.

What is wrong here is not the calculation itself. The error is to conclude that there is a causal relationship in what is just an absurd coincidence. There are different underlying causes that, erroneously, make it look like there is a covariance where one will continue to mirror the other.

Covariance is the measure of the correlation, i.e. the linear graph that shows the relationship. How much do two datasets vary from each other, and how much do they correlate? The covariance can be positive (the graphs follow each other) or negative (every time one graph swings up, the other goes down).

Justin Bieber’s age showed an almost perfect correlation with falling cholesterol levels in the population—but this trend took a U-turn as soon as Facebook was launched. Not only is this another silly example of an apparent correlation without a causal relationship. Here we also go from having a negative to a positive covariance, as the cholesterol first dropped, and then rose, in perfect rhythm with the singer’s age.

Such datasets can also be represented more simply, with a correlation coefficient, which we mentioned in connection with Pearson. This uses both the standard deviations of the datasets and their covariance, to find a “real” indicator of correlation. It is in such a calculation that the spurious examples above would quickly fall apart.

This is how statistics are used to verify data and datasets, and ensure that you can trust them—and ultimately use the knowledge to make decisions that have real-world consequences.

This is closely related to probability calculation, and that’s the next thing we’re going to look at.